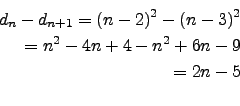
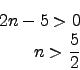
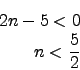
![]() steigt unbegrenzt an, ab welcher Platzziffer
steigt unbegrenzt an, ab welcher Platzziffer ![]() sind die Folgenglieder gr"oßer
als
sind die Folgenglieder gr"oßer
als ![]() ?
?
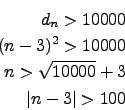
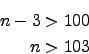
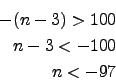
2. Fall unl"osbar f"ur
![]() !
!
![]() f"ur alle
f"ur alle ![]() .
.
Wenn ![]() unbeschr"ankt, dann
unbeschr"ankt, dann ![]() streng monoton.
streng monoton.
![]() unb.
unb.
![]() mon.
mon.
Die Folge ![]() steigt streng monoton und trotzdem steigt sie nicht unbegrenzt an.
Sie scheint sich der Zahl 1 ``anzun"ahern''.
steigt streng monoton und trotzdem steigt sie nicht unbegrenzt an.
Sie scheint sich der Zahl 1 ``anzun"ahern''.
Man sagt: Die Folge ![]() hat den Grenzwert 1.
hat den Grenzwert 1.
Dieser Wert wird von den Folgendgliedern beliebig angen"ahert, d.h. der
Abstand der Folgendglieder zum Grenzwert 1 unterschreitet jede noch so
kleine positive Zahl.
Ab welcher Platzziffer ![]() ist der Abstand der Folgenglieder kleiner als
ist der Abstand der Folgenglieder kleiner als
![]() ?
?
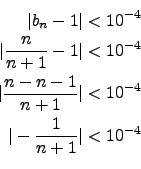
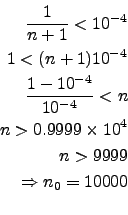
F"ur alle
![]() ist der Abstand der Folgenglieder
zum Grenzwert 1 kleiner als
ist der Abstand der Folgenglieder
zum Grenzwert 1 kleiner als ![]() !
!
![]() und
und
![]() seien vorgegeben
seien vorgegeben
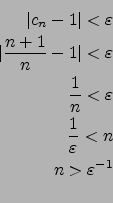
![]() F"ur alle
F"ur alle
![]() gilt:
gilt:
![]() .
.