z.B.
![]()
d.h.
![]()
Wir wissen bereits:
![]()
![]() kann hier in einer beliebigen Art u. Weise unbegrenzt enwachsen.
kann hier in einer beliebigen Art u. Weise unbegrenzt enwachsen.
![\includegraphics[]{graphen/00010}](img165.png)
![]() hat an der Stelle
hat an der Stelle ![]() eine Definitionsl"ucke.
eine Definitionsl"ucke.
![\includegraphics[]{graphen/00011}](img171.png)
Was geschieht f"ur ![]() ?
?
Vorsichtshalber beschr"anken wir uns auf die Betrachtung f"ur alle ![]() !
!
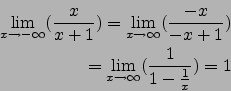
In all diesen F"allen ist die ![]() -Achse waagrechte Asymptote der Funktionsgraphen.
-Achse waagrechte Asymptote der Funktionsgraphen.
![\includegraphics[]{graphen/00012}](img186.png)
F"ur sehr große ![]() gilt:
gilt:
d.h. f"ur ![]() n"ahert sich der Graph von
n"ahert sich der Graph von ![]() der Geraden
der Geraden
![]() beliebig an.
beliebig an.
![]() ist die Funktionsgleichung einer sogenannten
schiefen Asymptote.
ist die Funktionsgleichung einer sogenannten
schiefen Asymptote.