![]() hat an der Stelle
hat an der Stelle ![]() eine Definitionsl"ucke.
Hat Graph
eine Definitionsl"ucke.
Hat Graph ![]() fort eine senkrechte Asymptote?
fort eine senkrechte Asymptote?
x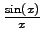
0
0.239
0.455
0.841
0.960
0.990
0.998
![\includegraphics[]{graphen/00013}](img199.png)
Mit Hilfe diser beiden Eigenschaften kann man ganz bequem und elegant
eine neue, l"uckenlose Funktion basteln, deren Graph an der Stelle
![]() nicht unterbrochen ist, sondern durchgezeichnet werden kann.
nicht unterbrochen ist, sondern durchgezeichnet werden kann.
Anschaulich: Man kann den Graphen von ![]() ohne Absetzen durchzeichnen.
ohne Absetzen durchzeichnen.
Man sagt: Wir haben ![]() an der Stelle
an der Stelle ![]() stetig fortgesetzt.
stetig fortgesetzt.
![]() ist eine abschnittsweise definierte Funktion.
ist eine abschnittsweise definierte Funktion.
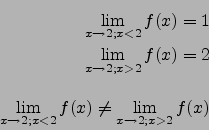
![]() ist an der Stelle
ist an der Stelle ![]() nicht stetig fortsetzbar!
nicht stetig fortsetzbar!
![]() ist an der Stelle
ist an der Stelle ![]() fortsetzbar, kann aber damit nie stetig
werde an der dieser Stelle.
fortsetzbar, kann aber damit nie stetig
werde an der dieser Stelle.
z.B.
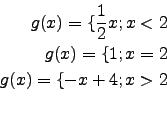
![]() hat an der Stelle
hat an der Stelle ![]() eine endliche Sprungstelle.
eine endliche Sprungstelle.
![]()
![]() existiert nicht
existiert nicht
![]() nicht stetig fortsetzbar an der Stelle
nicht stetig fortsetzbar an der Stelle ![]() .
.
![]() ist aber fortsetzbar z.B.
ist aber fortsetzbar z.B.
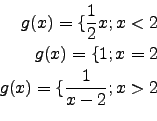
![]() hat an der Stelle
hat an der Stelle ![]() eine unendliche Sprungstelle.
eine unendliche Sprungstelle.