


Next: Die Ableitungsfunktion
Up: Funktionen
Previous: Gleichung der Normalen
Contents
Subsections
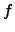 ist an der Stelle
ist an der Stelle 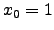 stetig
stetig
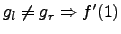 existiert nicht!
existiert nicht!
 f ist an der Stelle
f ist an der Stelle 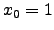 nicht differenzierbar.
nicht differenzierbar.
Anschaulich bedeutet das: Graph f hat an der Stelle 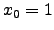 einen Knick.
einen Knick.
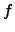 ist unstetig an der Stelle
ist unstetig an der Stelle 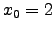 , da
, da
existiert nicht, da
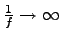
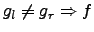 ist an der Stelle
ist an der Stelle 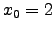 nicht
differenzierbar.
nicht
differenzierbar.
Eine Funktion 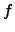 sei in
sei in
![$\mathbb{D}_f=[a;b]$](img301.png) definiert.
definiert.
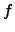 heißt differenzierbar an der Stelle
heißt differenzierbar an der Stelle ![$x_0 \in ]a;b[$](img302.png) , wenn
, wenn
Sprungstelle 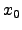 (unstetig an der Stelle
(unstetig an der Stelle
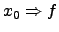 nicht
differenzierbar an der Stelle
nicht
differenzierbar an der Stelle 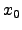
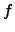 stetig an der Stelle
stetig an der Stelle 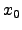 , jedoch mit ``Knick''
, jedoch mit ``Knick'' 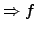 nicht differenzierbar an der Stelle
nicht differenzierbar an der Stelle 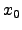
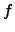 stetig an der Stelle
stetig an der Stelle 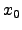 und ``glatt''
und ``glatt'' 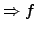 ist
differenzierbar an der Stelle
ist
differenzierbar an der Stelle 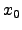
Ist 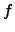 an der Stelle
an der Stelle 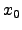 stetig, dann ist nicht sicher, ob
stetig, dann ist nicht sicher, ob 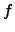 dort
auch differenzierbar ist.
dort
auch differenzierbar ist.
Stetigkeit
 Differenzierbarkeit
Differenzierbarkeit
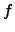 nicht differenzierbar an der Stelle
nicht differenzierbar an der Stelle
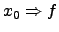 ist stetig
oder unstetig an der Stelle
ist stetig
oder unstetig an der Stelle 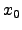
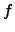 differenzierbar an der Stelle
differenzierbar an der Stelle
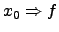 stetig an der Stelle
stetig an der Stelle
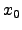
Stetigkeit ist eine notwendige, aber nicht hinreichende
Bedingung für Differenzierbarkeit.
Differenzierbarkeit ist eine hinreichende, aber nicht
notwendige Bedingung für die Stetigkeit.
Analytische Begründung für die Aussage
Differenzierbarkeit 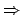 Stetigkeit:
Stetigkeit:
existiert
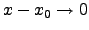 für
für 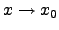
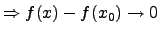 für
für 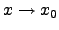 , da
, da 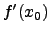 existiert.
existiert.
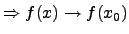 für
für 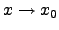
d.h.
 (q.e.d)
(q.e.d)



Next: Die Ableitungsfunktion
Up: Funktionen
Previous: Gleichung der Normalen
Contents
Michael Arndt
2006-04-07
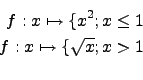
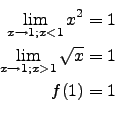
![]()
![]() ist an der Stelle
ist an der Stelle ![]() stetig
stetig
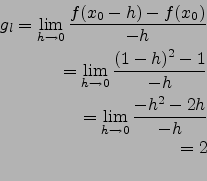
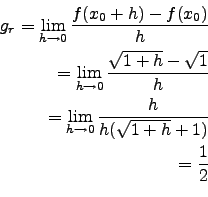
![]() existiert nicht!
existiert nicht!
![]() f ist an der Stelle
f ist an der Stelle ![]() nicht differenzierbar.
nicht differenzierbar.
![]() einen Knick.
einen Knick.
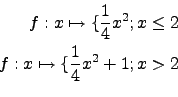
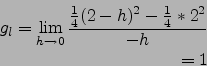
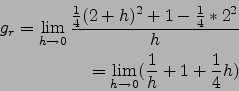
![]() ist an der Stelle
ist an der Stelle ![]() nicht
differenzierbar.
nicht
differenzierbar.
![]() sei in
sei in
![]() definiert.
definiert.
![]() heißt differenzierbar an der Stelle
heißt differenzierbar an der Stelle ![]() , wenn
, wenn
![]() Differenzierbarkeit
Differenzierbarkeit
![]() differenzierbar an der Stelle
differenzierbar an der Stelle
![]() stetig an der Stelle
stetig an der Stelle
![]()
![]() für
für ![]()
![]() (q.e.d)
(q.e.d)