


Next: Die Summenregel
Up: Funktionen
Previous: Die Ableitungsfunktion
Contents
Subsections
n Faktoren 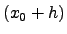
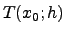 ist ein ganzrationaler Term
ist ein ganzrationaler Term
Analog zum rechtsseitigen Grenzwert
Die Potenzregel gilt auch für rationale Exponenten
(ohne Beweis!).
Michael Arndt
2006-04-07
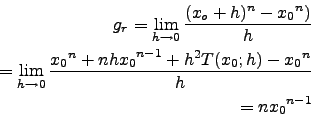
![]() ist ein ganzrationaler Term
ist ein ganzrationaler Term