


Next: Hinreichendes Kriterium für eine
Up: Funktionen
Previous: Extremstellen und Extremwerte einer
Contents
Subsections
 sei auf einem Intervall
sei auf einem Intervall
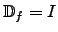 definiert.
definiert.
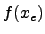 heißt relatives Maximum der Funktion, wenn es eine
Umgebung
heißt relatives Maximum der Funktion, wenn es eine
Umgebung 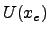 gibt, so dass für alle
gibt, so dass für alle
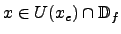 gilt:
gilt:
Gilt diese Bedingung für alle
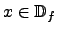 , so ist
, so ist
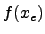 sogar absolutes Maximum.
sogar absolutes Maximum.
S.o. ..., so dass gilt:
Wenn eine Funktion 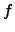 eine Extremstelle
eine Extremstelle 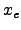 hat,
dann hat der Graph an dieser Stelle
(
hat,
dann hat der Graph an dieser Stelle
(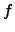 ist dort also
differenzierbar) oder
ist dort also
differenzierbar) oder
(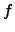 ist dort also nicht
differenzierbar) oder
ist dort also nicht
differenzierbar) oder
(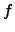 ist dort also nicht
differenzierbar) oder
ist dort also nicht
differenzierbar) oder
(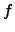 ist dort also nicht
differenzierbar)
ist dort also nicht
differenzierbar)
Zur Vereinfachung beschränken wir uns ab sofort auf
Funktionen, die an der Stelle 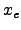 differenzierbar sind.
differenzierbar sind.
Eine Funktion 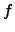 sei an einer Stelle
sei an einer Stelle ![$x_e \in ]a;b[$](img412.png) differenzierbar.
Wenn
differenzierbar.
Wenn 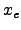 eine Extremstelle ist, dann gilt
eine Extremstelle ist, dann gilt 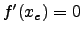 .
.
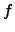 ist an der Stelle
ist an der Stelle ![$x_e \in ]a;b[$](img412.png) differenzierbar und
differenzierbar und
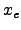 sei Extremstelle.
sei Extremstelle.
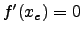
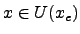
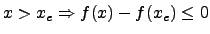 nach Definition des Maximums;
nach Definition des Maximums;
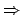 Sekantensteigung:
Sekantensteigung:
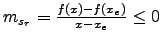
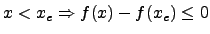 nach Definition des Maximums;
nach Definition des Maximums;
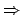 Sekantensteigung:
Sekantensteigung:
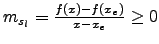
Diese beiden Grenzwerte müssen gleich sein!
Da 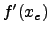 existient (nach Voraussetzung) gilt:
existient (nach Voraussetzung) gilt: 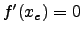 q.e.d.
q.e.d.
Wenn 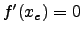 dann ist
dann ist 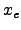 eine Extremstelle?
eine Extremstelle?
![\includegraphics[]{graphen/00021}](img425.png)
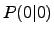 ist ein Sattelpunkt,
ist ein Sattelpunkt, 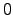 ist Sattelstelle.
ist Sattelstelle.
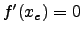 ist notwendig, aber nicht hinreichend
für das Vorhandensein einer Extremstelle!
ist notwendig, aber nicht hinreichend
für das Vorhandensein einer Extremstelle!



Next: Hinreichendes Kriterium für eine
Up: Funktionen
Previous: Extremstellen und Extremwerte einer
Contents
Michael Arndt
2006-04-07
![]() , so ist
, so ist
![]() sogar absolutes Maximum.
sogar absolutes Maximum.
![]() nach Definition des Maximums;
nach Definition des Maximums;
![]() Sekantensteigung:
Sekantensteigung:
![]()
![]() nach Definition des Maximums;
nach Definition des Maximums;
![]() Sekantensteigung:
Sekantensteigung:
![]()
![]() existient (nach Voraussetzung) gilt:
existient (nach Voraussetzung) gilt: ![]() q.e.d.
q.e.d.
![\includegraphics[]{graphen/00021}](img425.png)
![]() ist ein Sattelpunkt,
ist ein Sattelpunkt, ![]() ist Sattelstelle.
ist Sattelstelle.