Exponentialfunktionen

Beispiel 1

Ein Anfangskapital soll $n$ Jahre zu einem Zinssatz von $p\%$ angelegt werden. Die Zinsen werden jährlich dem vorhandenen Kapital hinzugefügt. Bestimme die Wachstumsfunktion $K(n)$

$$\begin{eqnarray*} K(0)=K_0\\ K(1)=K_0 + K_0 * \frac{p}{100} = K_0(1+\frac{p}{10... ...)(1+\frac{p}{100})\\ =K_0(1+\frac{p}{100})(1+\frac{p}{100})\\ \end{eqnarray*}$$

$\vdots$

$$K(n)=K_0*(1+\frac{p}{100})^n$$

$$q=1+\frac{p}{100} > 1 \Rightarrow \lq\lq Wachstumsfaktor''$$

$$\Rightarrow K(n) = K_0 * q^n$$

Beispiel 2

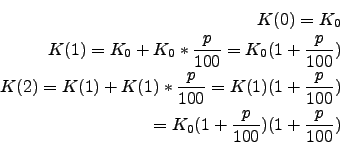
Eine Bakterienkultur, die auf einem genügend großem Nährmedium angelegt wird wächst nach einem ganz bestimmten Gesetz: Das Zeitintervall, in der sich die kulzurbedeckte Fläche $A$ verdoppelt (verdreifacht, ...) ist immer gleich, egal wieviele Bakterien momentan vorhanden sind. Bestimme die Wachstumsfunktion $A(t)$

$t_2$: Verdopplungszeit

$$\begin{eqnarray*} A(0)=A_0\\ A(t_2)=2A_0\\ A(2*t_2)=4A_0\\ \end{eqnarray*}$$

$\vdots$

$$A(nt_2)=A_0*2^n$$

$$nt_2 = t \Rightarrow n=\frac{t}{t_2} \Rightarrow A(t)=A_0*2^\frac{t}{t_2}$$

Beispiel 3

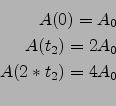
Ein radioaktives Element x besitzt eine Halbwertszeit von $t_H$, d.h. jedes Zeitintervall $t_H$ zerfällt die Hälfte der im Moment vorhandenen x-Kerne (Anzahl $N$). Zerfallsfunktion:

$$N(t)=N_0*(\frac{1}{2})^\frac{t}{t_H}$$

Definition

$$f:x\mapsto a*b^x; (a\in \mathbb{R}\backslash\lbrace 0 \rbrace; b \in \mathbb{R}^+ \backslash\lbrace 1 \rbrace)$$

heißt Exponentialfunktion zur Basis $b$. $\mathbb{D}=\mathbb{R}$

Spezialfall

$$a=1 \Rightarrow f(x)=b^x$$

$0<b<1 \Rightarrow$ Zerfallsfunktion
$b>1 \Rightarrow$ Wachstumsfunktion

Eigenschaften von $f(x)=b^x$

1. $0<b<1 \Rightarrow$ Graph $f$ ist streng monoton fallend
   $b>1 \Rightarrow$ Graph $f$ ist streng monoton steigend
2. $S_y(0\vert 1)$ für alle $b\in\mathbb{R}^+\backslash\lbrace 1\rbrace$
3. $0<b<1 \Rightarrow$ x-Achse ist Asymptote für $x\to+\infty$
   $b>1 \Rightarrow$ x-Achse ist Asymptote für $x\to-\infty$
4. $\mathbb{W}=\mathbb{R}^+$ für alle $b\in\mathbb{R}^+\backslash\lbrace 1\rbrace$
5. $x_0 \in \mathbb{D}, h>0$
   $f(x_0+h)=b^{x_0+h}=b^{x_0}*b^{h} = f(x_0)*f(h)$
   ``Funktionalgleichung einer Exponentialfunktion''
6. $f_1:x\to b^x$ und $f_2:x\to (\frac{1}{b})^x$
   Behauptung: Graph $f_1 \leftarrow$ Spiegelung an der Y-Achse $\rightarrow$ Graph $f_2$
   Beweis: $f_1(x)=b^x=\frac{1}{b^{-x}}=(\frac{1}{b})^{-1}=f_2(-x)$

Die $e$-Funktion

$f:x\to e^x$ mit $f'(x)=f(x)$

Satz: $h:x\to a*e^x; (a\in\mathbb{R}\backslash\lbrace 0 \rbrace)$ sind die einzigen Funktionen mit $h'(x)=h(x)$