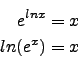![]() ist die Hochzahl, mit der man
ist die Hochzahl, mit der man ![]() potenzieren muss, um
potenzieren muss, um
![]() zu erhalten.
zu erhalten.
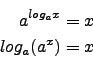
Definition: Eine Funktion ![]() ist umkehrbar auf dem Intervall
ist umkehrbar auf dem Intervall
![]() , wenn für alle
, wenn für alle
![]() gilt:
gilt:
![]()
Satz:
![]() ist streng monoton wachsend (fallend) für alle
ist streng monoton wachsend (fallend) für alle
![]() ist umkehrbar auf
ist umkehrbar auf ![]() .
.
Bekannt:
![]() ist für
ist für ![]() streng monoton fallend und für
streng monoton fallend und für ![]() streng monoton wachsend.
streng monoton wachsend.
![]()
Es existiert eine Umkehrfunktion ![]() von
von ![]() !
!
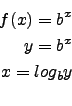
Vertauschen von ![]() und
und ![]() :
:
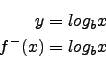
``Logarithmusfunktion''
![\includegraphics[]{graphen/00027}](img522.png)
![]()
Es gilt: