Das Zufallsexperiment ist ein Laplace-Experiment
Laplace-Experiment mit
![]() und
und
![]()
Beweis:
Aus 1 und 2
![]()
Laplace-Experiment mit
![]() und
und
![]() und
und
![]() mit
mit
![]()
Beweis:
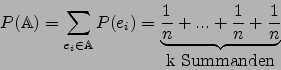
Stabdiagramm:
Wahrscheinlichkeitsverteilung ( = Gleichverteilung)
ABER! Kein Laplace-Experiment, da
![]()
Verfeinerung der Ergebnismenge
Änderung des Merkmals
![]() , Zufallsgröße
, Zufallsgröße ![]() , mit
, mit ![]() = Augensumme
= Augensumme
Stabdiagramm:
Symetrische Verteilung
![]() -Durchführungen eines Zufallsexperiments,
-Durchführungen eines Zufallsexperiments, ![]() -maliges Eintreten
des Ereignisses
-maliges Eintreten
des Ereignisses ![]() .
.
Computersimulation: Doppelwürfelexperiment mit ![]() Versuchen.
Versuchen.
![]() .
.
Erkenntnis: für sehr große ![]() gilt:
gilt:
![]() ,
wobei
,
wobei ![]() relative Häufigkeit und
relative Häufigkeit und ![]() Wahrscheinlichkeit eines Ereignisses ist.
Wahrscheinlichkeit eines Ereignisses ist.