


Next: Erwartungswert einer Zufallsgrößen
Up: Stochastik
Previous: Exkurs: Kombinatorik
Contents
Subsections
Bei vielen Untersuchungen (Stichproben) spielen Zufallsexperimente mit
nur zwei Ergebnissen eine Rolle: z.B. Münzwurf (Kopf, Zahl),
Würfel (6, nicht 6), Qualitätskontrolle (defekt, nicht defekt).
Treffer (T) und Niete (N)
- Ein Zufallsexperiment mit
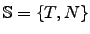 , also
, also
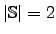 , ist ein Bernoulli-Experiment mit der
Trefferwahrscheinlichkeit
, ist ein Bernoulli-Experiment mit der
Trefferwahrscheinlichkeit 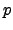 .
.
- Eine Bernoulli-Kette der Länge
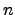 ist ein Zufallsexperiment, das aus
ist ein Zufallsexperiment, das aus
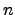 unabhängigen Bernoulli-Experimenten mit der selben
Trefferwahrscheinlichkeit
unabhängigen Bernoulli-Experimenten mit der selben
Trefferwahrscheinlichkeit 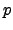 besteht.
besteht.
N Kugeln  S schwarze Kugeln
S schwarze Kugeln 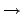 (N-S) weiße Kugeln
(N-S) weiße Kugeln
n-mal Ziehen mit Zurücklegen
X=k mit k=Anzahl der Treffer (= schwarze Kugel)
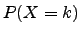 Wahrscheinlichkeit für k Treffer.
Wahrscheinlichkeit für k Treffer.
Trefferwahrscheinlichkeit 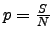 , Wahrscheinlichkeit für Niete
, Wahrscheinlichkeit für Niete
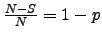
=3in
stochastik/baumdiagramm_bernoulli_1
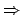
``Formel von Bernoulli''
-
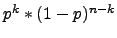 Wahrscheinlichkeit eines Pfades mit k Treffern
Wahrscheinlichkeit eines Pfades mit k Treffern
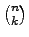 Anzahl der Pfade mit k Treffern
Anzahl der Pfade mit k Treffern
-
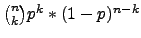 Wahrscheinlichkeit aller Pfade
mit k Treffern
Wahrscheinlichkeit aller Pfade
mit k Treffern
Die Wahrscheinlichkeitsverteilung 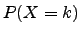 mit
mit
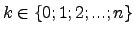 einer Bernoulli-Kette der Länge
einer Bernoulli-Kette der Länge 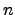 mit der Trefferzahl
mit der Trefferzahl 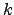 und der
Trefferwahrscheinlichkeit
und der
Trefferwahrscheinlichkeit 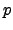 ist eine Binomialverteilung
ist eine Binomialverteilung 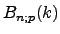 mit den Parametern
mit den Parametern 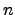 ,
, 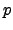 und
und 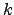 .
.
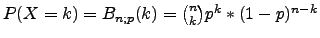
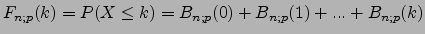 heißt
summierte Binomialverteilung mit den Parametern
heißt
summierte Binomialverteilung mit den Parametern 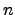 und
und 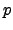 .
.
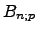 und
und 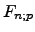 werden in Mathebüchern oft als Tabellen vorgegeben!
werden in Mathebüchern oft als Tabellen vorgegeben!
Die summierte Wahrscheinlichkeit eigent sich besonders dann, wenn die
k-Werte in einem zusammenhängenden Bereich liegen:



Next: Erwartungswert einer Zufallsgrößen
Up: Stochastik
Previous: Exkurs: Kombinatorik
Contents
Michael Arndt
2006-04-07
![]()
![]() mit
mit
![]() einer Bernoulli-Kette der Länge
einer Bernoulli-Kette der Länge ![]() mit der Trefferzahl
mit der Trefferzahl ![]() und der
Trefferwahrscheinlichkeit
und der
Trefferwahrscheinlichkeit ![]() ist eine Binomialverteilung
ist eine Binomialverteilung ![]() mit den Parametern
mit den Parametern ![]() ,
, ![]() und
und ![]() .
.
![]() heißt
summierte Binomialverteilung mit den Parametern
heißt
summierte Binomialverteilung mit den Parametern ![]() und
und ![]() .
.