Standardabweichung

Wiederholung: Erwartungswert

Zufallsgröße $x=x_i$ mit $x_i \in \lbrace x_i, ..., x_n \rbrace$

$$\Downarrow$$

Wahrscheinlichkeitsverteilung von $X$:

$x_i$ $x_1$ $x_2$ ... 		 $x_n$ 

$P(X=x_i)$ ... 		 ... 		 ... 		 ... 

$$\Rightarrow \sum\limits_{i=1}^n P(X=x_i)=1$$

$$\Downarrow$$

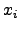
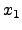
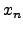
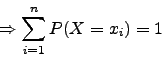
Erwartungswert $E(X)$ (zu erwartender Mittelwert bei einem sehr großen Stichprobenumfang)

$$E(X)=x_i*P(X=x_i)+...+x_n*P(X=x_n)$$

Maß für ``mittlere Abweichung''

Gesucht: Maß für die ``mittlere Abweichung'' oder die ``Streuung'' der Werte von $X$ vom Erwartungswert $E(X)$.

Definition Varianz und Standardabweichung

Zufallsgröße $X=x_i$ mit $x_i \in \lbrace x_i, ..., x_n \rbrace$ und $E(X)=µ$

1. $V(X)=(x_1-µ)^2*P(X=x_1)+...+(x_n-µ)^2*P(X=x_n)$ heißt Varianz von $X$
2. $\sigma(X)=\sqrt{V(X)}$ heißt Standardabweichung von $X$

Beachte: $V(X)=\sigma(X)^2 = \sigma^2$

Satz zur Standardabweichung

Eine binomial verteilte Zufallsgröße $X$ mit den Parametern $n$ und $p$

$$\Rightarrow \sigma(X) = \sqrt{np*(1-p)}$$

(ohne Beweis)